（2017年10月21日にQiitaにて執筆した記事をこちらに転載しています。）
はじめに
この記事ではビットコインで使われているビットコインアドレスを自分の手で作る手順を紹介しています。ビットコインアドレスを作ることを通して、ビットコインに対する技術的な理解を深めることが目的です。
ビットコインアドレスを作る手順は大まかに言うと以下のようになっており、この記事では各手順を順番に説明していきます。
- 秘密鍵を作る
- 公開鍵を秘密鍵から作る
- 公開鍵のハッシュを公開鍵から作る
- ビットコインアドレスを公開鍵ハッシュと公開鍵から作る
ビットコインアドレスとは何か
ビットコインアドレスとは、ビットコインを誰かが誰かに送付するときに宛先として利用するものです。例えば以下のような形をしています（ちなみにこのアドレスは堀江貴文さんがTwitterにて公開しているビットコインアドレスです。）
1G2jt5WeGhqWtDKEkcKY2GrZKjfYsuiVxX
個人間のビットコインアドレスのやり取りにせよ、実店舗やネットでのビットコインを使った買い物にせよ、ビットコインの所有権がある人から別の人に移るとき、基本的には新しい所有者のビットコインアドレスへビットコインが送付されるという形をとります。
この記事では触れませんが、このようにビットコインの所有権がある所有者から次の所有者に移されることをトランザクションと言います。トランザクションにも興味があれば、下部の参照セクションにある記事も読んでみて下さい。
秘密鍵を作る
まず秘密鍵を作ります。秘密鍵とは何かと言いますと、何も面白くない答えですがただの整数です。大雑把に言えばですが、
から
整数のどれかであればどれでもOKです。実はよりもわずかに小さい数が上限なのですが、それは後程詳しく述べます。
ここで大事なことを言います。あなたの秘密鍵が誰かに知られたら所有しているコインはすべて奪われますし、もし失くすなり忘れるなりしてしまったらコインは永久埋蔵金になります。
よって秘密鍵は充分に不規則な乱数で、十分に大きい数を作らなければなりません。また大切に、かつ人目に付かないところに保管しておかなければなりません。本当に大事なものです。
上でからの間ならどれでも良いと書いたのはあくまで理論上の話で、例えばあなたの秘密鍵が5だったらあっという間に誰かにビットコインを奪われてしまうと思った方がいいです。
ちなみにとは以下のように78桁にも及ぶとてつもなく大きな数で、観測可能な宇宙にある原子の数とかそういう値に匹敵するくらいの大きさの数です。これだけ大きければ、例え全人類がビットコインを使うようになったとしても十分だと言えるでしょう。
この記事中では、今まさにこの行を書いている時点での日付と時間にちなんで2017101920171019を秘密鍵に使う整数としたいと思います。以下、この秘密鍵をkと呼びます。
公開鍵を秘密鍵から作る
次に公開鍵を秘密鍵から作ります。
公開鍵の作成手順は、この記事で紹介している一連のビットコインアドレス作成手順の中で一番複雑であり、一番面白い所です。
まずは公開鍵について、以下の大事な点を抑えておきましょう。
- 公開鍵とは
のようにふたつの整数のペアである
- 公開鍵は秘密鍵から計算によって求められるが、公開鍵から秘密鍵を計算したり推測したりすることは現実的にはできない
- よって公開鍵は人目に触れても安全（ただし見せる理由はない）
では、公開鍵の作成手順の説明に入ります。
楕円曲線暗号と楕円曲線DSA（楕円曲線デジタル署名アルゴリズム）
ビットコインの公開鍵は、Secp256k1という楕円曲線暗号を用いたデジタル署名アルゴリズムを使い、秘密鍵から計算されて作られます。
ここで個々の理論について突っ込んで説明するスペースも力量もありませんので、あくまでビットコインで使われているSecp256k1に着目して説明したいと思います。
Secp256k1
Secp256k1とは何かと言いますと、簡単に言ってしまえば点の集合です。どんな点の集合かと言いますと、以下の式に従う点の集合です。
なんだかすごい数字が出てきましたね。このmodの横にある一連の数字を面倒くさいので
と呼ぶことにします。このはどうやら素数らしいのですが、上の秘密鍵の説明のところで「よりわずかに小さい数」と書いたのがこのです。
これがどんな点の集合になるのか図にして見てみたいところですが、あまりにも数が大きくて色々な意味で無理なので、pをちょっと小さい素数にして3パターン図にしてみました（以下はRのプログラムです。）
p <- 17
xlist <- c()
ylist <- c()
for (x in 1:p) {
for (y in 1:p) {
if (((x^3 + 7 - y^2) %% p) == 0) {
xlist[length(xlist) + 1] <- x
ylist[length(ylist) + 1] <- y
}
}
}
plot(xlist,
ylist,
type = "p",
main = sprintf("(x^3 + 7 - y^2) mod %d == 0", p),
xlab = "x",
ylab = "y",
)
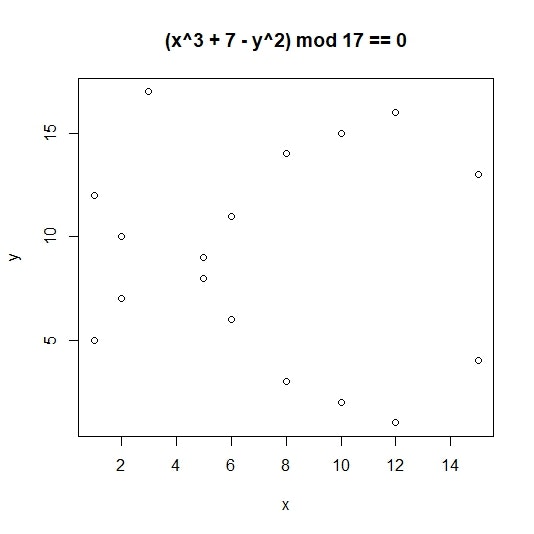
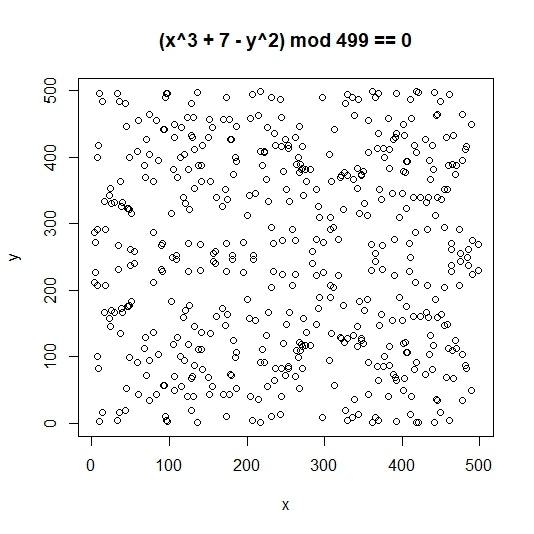
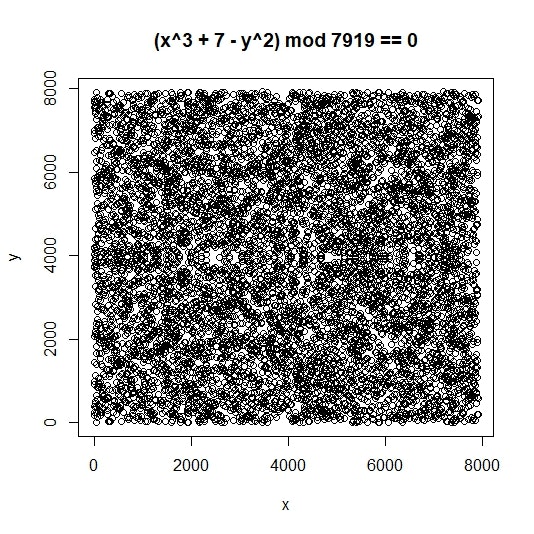
どうでしょう、何となく雰囲気が掴めたでしょうか？が7919でももうかなりぐちゃぐちゃなので、Secp256k1が定義している巨大素数を使ったら大変なことになってしまいそうです。
さて計算で公開鍵を求める前にイメージしておいて欲しいのが、この膨大な点のどれかひとつがあなたの公開鍵になるということです。公開鍵は二つの整数のペアだと上で書きましたが、このどれかひとつの点の座標
があなたの公開鍵になります。
生成元G
上でSecp256k1は定義された式に従う点の集合だと書きましたが、実はもうひとつSecp256k1がして定義いるものがあります。それが生成元です。
生成元とは何かと言いますと、これも要するに膨大に存在する点の中のあるひとつです。この点を（まさに文字通り）起点として公開鍵の計算を行うので生成元（Generator Point）と呼ばれます。以下、この生成元を
と呼びたいと思います。
以下のPythonプログラムで、生成元の具体的な値と、それがきちんと
に従っていることが確認できます。
p = 2**256 - 2**32 - 2**9 - 2**8 - 2**7 - 2**6 - 2**4 - 1
Gx = 0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
Gy = 0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8
print("p = ", p)
print("Gx = ", Gx)
print("Gy = ", Gy)
print("Gy^2 - Gx^3 - 7 mod p = ",(Gy**2 - Gx**3 - 7) % p)
出力結果です。
p = 115792089237316195423570985008687907853269984665640564039457584007908834671663
Gx = 55066263022277343669578718895168534326250603453777594175500187360389116729240
Gy = 32670510020758816978083085130507043184471273380659243275938904335757337482424
Gy^2 - Gx^3 - 7 mod p = 0
の
も
も非常に大きい数であることが分かります。またそののとを
に代入してみたところ答えが
になることも確認できました。
生成元Gと秘密鍵kから公開鍵を計算する
ではいよいよ公開鍵を計算によって求めます。ここが一番の肝です。
まず単刀直入に言ってしまうと、公開鍵を求めるには生成元Gを秘密鍵kを使ってk倍してやればいいだけです。つまり求めたい公開鍵をKとすると
ということになります。なんて簡単なんでしょう。
しかし実はこれは単純な掛け算をすれば良いということではないので、のとにそれぞれkをかけて
と
にすれば良いということではありません。
ではどのように演算しなければならないかというと、楕円曲線上のスカラー倍算（スカラー倍算というのは、要はある整数と掛けること）をする必要があります。
この記事の中で楕円曲線上の演算の話を書きだすと記事の量がそれこそ倍算されてしまうので思い切って省略させて頂きたいと思いますが、以下のサイトを参考にしてみて下さい。特にQiitaの記事は分かり易く書かれていてお勧めです。
リンク先のサイトを読んでいただけたかとは思うのですが、一応すごく簡単に自分の言葉でも説明しておきます。
ちなみにどのサイトの説明でも楕円曲線が、楕円ではないにせよ「曲線」だと扱われて説明されていますが、あくまで我々が相手にしているのは点の集合のはずです。それをお忘れなく。
楕円曲線上で加算する場合
楕円曲線上の点Pと点Qの足し算した結果を点Rとすると、点Pと点Qを通る直線と（想像上の）楕円曲線が交わるもうひとつの点、それをx軸で反転させた（つまりその点のyを-1倍した）点をがRとなると定義します。
数式で説明します。ある点P（座標は
とする）とある点Q（座標はtex:(x_q,y_q)])を足した結果の点R（座標は
)は以下のように求められます。
は単純に点Pと点Qを通る直線の傾きですね。続く
と
を求める式の詳細は、ここでは触れません（ごめんなさい。）
ちなみにここで注意して欲しいことがあります。の中に分数、つまり割り算が出てきますが、これは普通に割り算をしてしまっては駄目です。なぜかと言うと我々はmodの世界にいるからです。この割り算については以下の記事にまとめましたので参考にして下さい。
を求める式の横にも
とか書いた方が良いのかもしれません。
逆数を考慮するとを求める式は以下のように書き換えた方が良いでしょう。
割り算を逆数との掛け算に変換しているというのがポイントです。
楕円曲線上である点を2倍する場合
楕円曲線上のある点Pを2倍する場合、その点における（想像上の）楕円曲線の接線と、（またまた想像上の）楕円曲線が交わるもうひとつの点、それをx軸で反転させた点が
の結果だと定義します。
数式で書いてみます。の求め方が加算のときと違いますが、単に微分で直線の傾きを求めるようにしただけです。根本的にやっていることは変わりません。また、こちらでも割り算を逆数との掛け算に変換しています。
ここで突然
が出てきました。これはなんでしょうか。
上でビットコインで使われる楕円暗号DSA（デジタル署名アルゴリズム）はSecp256k1で、それはからなる点の集合を定義すると説明しました。
実は楕円曲線は一般的には
で定義されており、Secp256k1は
としています。このはそのなので、ここでは0となります。
楕円曲線上である点をスカラー倍する場合
これは加算と2倍算の組み合わせで出来ます。例えばある点Pを7倍したい場合、
の様に計算します。
ちなみにこの計算式、7の2進数表記が111であることから割り出せるという不思議なものなのです。詳しくはビットコインニュースの記事を読んで欲しいのですが、要するに
- そのスカラーを2進数にする
- 一番左のビットは無視
- 二番目のビットからは順番に、1だったら「2倍算してから同じ点を足す」、0だったら「ただ2倍算をする」
を繰り返して求めます。
もちろん足し算を繰り返しても求められるのですが、そうやると効率が悪く計算時間が長くかかってしまいます。覚えていますか？秘密鍵kは安全の為にある程度大きい必要があります。
楕円曲線上の演算を行うプログラム
ではいよいよプログラムによって公開鍵を秘密鍵から計算します。上述の内容を踏まえて、楕円暗号上の2点の加算、ある点の2倍算、そしてある点のスカラー倍算を実装します。以下のコードはC#です。
using System;
using System.Numerics;
namespace MakeBitcoinAddress
{
class ECPoint
{
public BigInteger x = 0;
public BigInteger y = 0;
}
static class Helper
{
public static BigInteger Mod(BigInteger value, BigInteger modulus)
{
var result = BigInteger.ModPow(value, 1, modulus);
return (result < 0) ? result + modulus : result;
}
public static BigInteger ModInverse(BigInteger value, BigInteger modulus)
{
if (value < 0)
{
value = Helper.Mod(value, modulus) + modulus;
}
BigInteger x = 0, y = 1, gcd = modulus;
BigInteger px = 1, py = 0, pgcd = value;
BigInteger temp = 0;
while (gcd > 0)
{
BigInteger quotient = pgcd / gcd;
temp = x;
x = px - quotient * temp;
px = temp;
temp = y;
y = py - quotient * temp;
py = temp;
temp = gcd;
gcd = pgcd - quotient * temp;
pgcd = temp;
}
return px;
}
public static string GetBinaryString(byte[] byteArray)
{
string result = string.Empty;
for (int i = 0; i < byteArray.Length; i++)
{
byte b = byteArray[i];
if ((b == 0) && (i == byteArray.Length - 1))
{
break;
}
string binaryString = Convert.ToString(b, 2);
if (i < byteArray.Length - 1)
{
while (binaryString.Length < 8)
{
binaryString = "0" + binaryString;
}
}
result = binaryString + result;
}
return result;
}
}
class Program
{
static BigInteger ModP = BigInteger.Parse("115792089237316195423570985008687907853269984665640564039457584007908834671663");
static ECPoint G = new ECPoint()
{
x = BigInteger.Parse("55066263022277343669578718895168534326250603453777594175500187360389116729240"),
y = BigInteger.Parse("32670510020758816978083085130507043184471273380659243275938904335757337482424")
};
static ECPoint ECAdd(ECPoint p, ECPoint q)
{
ECPoint result = new ECPoint();
BigInteger lambda = (q.y - p.y) * Helper.ModInverse((q.x - p.x), ModP);
result.x = BigInteger.Pow(lambda, 2) - p.x - q.x;
result.x = Helper.Mod(result.x, ModP);
result.y = lambda * (p.x - result.x) - p.y;
result.y = Helper.Mod(result.y, ModP);
return result;
}
static ECPoint ECDouble(ECPoint p)
{
ECPoint result = new ECPoint();
BigInteger lambda = (3 * BigInteger.Pow(p.x, 2)) * Helper.ModInverse((2 * p.y), ModP);
result.x = BigInteger.Pow(lambda, 2) - (2 * p.x);
result.x = Helper.Mod(result.x, ModP);
result.y = lambda * (p.x - result.x) - p.y;
result.y = Helper.Mod(result.y, ModP);
return result;
}
static ECPoint ECScalar(ECPoint p, BigInteger scalar)
{
ECPoint result = new ECPoint() { x = p.x, y = p.y };
string s = Helper.GetBinaryString(scalar.ToByteArray());
foreach(var c in s.Substring(1))
{
result = ECDouble(result);
if (c.Equals('1'))
{
result = ECAdd(result, p);
}
}
return result;
}
static bool IsOnSecp256k1(ECPoint p)
{
var answer = Helper.Mod((BigInteger.Pow(p.y, 2) - BigInteger.Pow(p.x, 3) - 7), ModP);
return (answer == 0);
}
static void Main(string[] args)
{
}
}
}
ではいよいよ上で定めた秘密鍵kから公開鍵Kを求めてみます。
static void Main(string[] args)
{
BigInteger k = 2017101920171019;
var publicKey = ECScalar(G, k);
Console.WriteLine(publicKey.x);
Console.WriteLine(publicKey.y);
Console.WriteLine(IsOnSecp256k1(publicKey));
}
以下が出力結果です。
36572950727085182085382801403406684418997739286809164939833038507156062366242
43641162618061335383666517243600726585787626462467298998793806674351551668099
True
これが正しいのかどうかはちょっと確かめるのが難しそうですが、とりえあえずSecp256k1で定義された式に従っている点が取得できました。私は個人的にはpを17にしてみて、手で計算できる範囲の値を使って色々とテストしてみたり、このWikiページに例として載っている値を使って計算したら合っているようだったので、ある程度は上手く動いていると見ています。
ちなみにここにきて気が付きましたが、どうやら.NETのMod計算は負の数を正の数に直さないようです。負の数のMod計算はプログラミング言語の実装によって流儀が違うので若干困りますね。今回は正の数で揃えたいと思っているので、Modの計算をHelperファンクションにて調整しています。
ようやく公開鍵を求めることが出来ました。次は公開鍵のハッシュを求めます。
公開鍵のハッシュを公開鍵から作る
ここから公開鍵のハッシュを求めます。
この文章を読んでいる方のほとんどはおそらくハッシュというものが何かということを理解していると思いますので、ハッシュの概念の説明は省きます。また個々のハッシュアルゴリズムそのものについての説明もこちらでは省きます。
公開鍵のハッシュを作る上で重要なポイントは、これも不可逆な一方向性の処理であり、公開鍵のハッシュから公開鍵を求めることは現実的には不可能ということです。
上で「公開鍵は人に見せても安全だが、見せる必要は基本的にはない」と書きましたが、ビットコインのやり取りで使われるのは、この公開鍵のハッシュであり、公開鍵ではありません。
SHA256とRIPEMD-160
公開鍵のハッシュはSHA256とRIPEMD-160というハッシュアルゴリズムを使って公開鍵（public key）から求められます。疑似的なプログラムで書くと、以下のように求められます。
PublicKeyHash = RIPEMD-160(SHA256(PublicKey))
簡単ですね。もちろんそれぞれのアルゴリズムの中身は多少複雑ではあると思いますが。
ハッシュアルゴリズムへの入力
次に公開鍵をどのようにSHA256の入力として与えればいいかを調べてみましょう。下のWikiページで説明されています。
Technical background of version 1 Bitcoin addresses – Bitcoin Wiki
入力は65バイトのバイト列にするべきのようで、以下のような形になるようです。
[1バイト 0x04][32バイト 公開鍵のxをビッグエンディアンで][32バイト 公開鍵のyをビッグエンディアンで]
ビッグエンディアンというのは、バイト列をどのような順番で並べるのかという話です。その他は特に問題ないかと思います。
ちなみに私は公開鍵はという整数のペアだという書き方をしましたけれど、上記のSHA256への入力値を指して公開鍵と呼んでいる場合が多いかもしれません。どちらにせよ概念的には同一です。
ビットコインのトランザクションのデータ量を削減するためなどの理由で、公開鍵のxだけを使った圧縮フォーマットも存在しています。これはyは実はxさえ分かっていれば簡単に求まることを利用しています。圧縮した場合は65バイトから33バイトにサイズを減らせます。この記事では圧縮フォーマットについては触れませんが、現実的にはこちらが使われるべきでしょう。
では、以下のコードで公開鍵のハッシュを求めてみます。以下のコードはC#で、ハッシュアルゴリズムについては.NETが提供しているライブラリを用いて行っています。スペースの節約の為、プログラムは一部のみ記載しています。
using System.Security.Cryptography;
using System.Text;
static class Helper
{
public static string ByteArrayToString(byte[] ba)
{
StringBuilder hex = new StringBuilder(ba.Length * 2);
foreach (var b in ba)
{
hex.AppendFormat("{0:X2}", b);
}
return hex.ToString();
}
}
class Program
{
static void Main(string[] args)
{
BigInteger k = 2017101920171019;
var publicKey = ECScalar(G, k);
byte[] inputBytes = new byte[65];
Array.Copy(new byte[1] { 0x04 }, 0, inputBytes, 0, 1);
byte[] x = publicKey.x.ToByteArray();
Array.Reverse(x);
byte[] y = publicKey.y.ToByteArray();
Array.Reverse(y);
Array.Copy(x, 0, inputBytes, 1, 32);
Array.Copy(y, 0, inputBytes, 33, 32);
SHA256 sha256 = new SHA256CryptoServiceProvider();
RIPEMD160Managed ripemd160 = new RIPEMD160Managed();
var publicKeyHash = ripemd160.ComputeHash(sha256.ComputeHash(inputBytes));
Console.WriteLine(Helper.ByteArrayToString(publicKeyHash));
}
}
以下、出力結果です。
976ED257CD5938560BA0C926AADB17927DB9E51B
RIPEMD-160は20バイトの出力を返すので当然ですが、公開鍵のハッシュはこのように20バイトとなっています。ビッグエンディアンでSHA256への入力を作る必要があることにご注意ください（私は.NETのBigIntegerのToByteArrayがリトルエンディアンを返すと知らずにトラブりました。）
ではいよいよ、最後の手順に進みたいと思います。
ビットコインアドレスを公開鍵ハッシュと公開鍵から作る
いよいよ最後にビットコインアドレスを作ります。
まず注意してもらいたいポイントがあります。今までの公開鍵の作成も、公開鍵のハッシュの作成も一方向的な手続きでした。つまり後戻りできないということです。おさらいになりますが、公開鍵から秘密鍵を逆に作成することも、公開鍵のハッシュから公開鍵を逆に作成することも、現実的には不可能です。
ですがこの最後の手順だけは違います。今からビットコインアドレスを公開鍵のハッシュから作成しますが、ビットコインアドレスを公開鍵のハッシュに戻すことは可能です。ビットコインアドレスを公開鍵から作成するのは単なるエンコーディングであり、暗号化もされなければハッシュ化もされていないので、デコーディングすれば元に戻せます。
別の言い方をすれば、公開鍵のハッシュとビットコインアドレスとは同じものですと言うことが出来ると思います。正直言うとこの最後の手順は、ただ利便性の為にデータの見た目を調整するだけの手順なのです。
バージョンバイトを先頭に追加する
まず公開鍵のハッシュの先頭にバージョンバイトと呼ばれる1バイトをくっつけます。
このバージョンバイトとは何かと言うと、このビットコインアドレスはビットコインの本当のネットワークで使われるのか、それともテスト用のネットワークで使われるのかを示す為のバイトです。
本当のネットワークであれば0x00を、テストのネットワークであれば0x6Fを付けることになっているようです。ここでは出来上がったビットコインアドレスを本当のネットワークで使いたいので0x00を付けます。
先頭に00が付き、現時点で以下の値が求められました。これを公開鍵のハッシュ（バージョンバイト付き）と呼びたいと思います。
00976ED257CD5938560BA0C926AADB17927DB9E51B
チェックサムを作る
ここで突然チェックサムの話が出てくるのですが、仕組みや使われ方はここでは説明ず、ここでは作られ方のみ説明したいと思います。
これもご存知かと思いますが、チェックサム（Check Sum）とはネットワークの途中で値が何かしら変更されてしまったり、打ち間違いなどで値が予期せぬものになったときにその誤りを検出するための仕組みです。
ここでのチェックサムは、上で求めた公開鍵のハッシュ（バージョンバイト付き）にSHA256を2回かけた結果の、先頭の4バイトと定義されています。
上のバージョンバイトと合わせて、C#で書くとこのような感じになります。
using System.Linq;
var pubKeyHashWithVersion = new byte[21];
Array.Copy(new byte[1] { 0x00 }, 0, pubKeyHashWithVersion, 0, 1);
Array.Copy(publicKeyHash, 0, pubKeyHashWithVersion, 1, 20);
var checkSum = sha256.ComputeHash(sha256.ComputeHash(pubKeyHashWithVersion)).Take(4).ToArray();
Base58
ビットコインではBase58またはBase58Checkと呼ばれるエンコーディング形式が使われています。
Base58というのは私も初耳でしたが、EメールのMIMEフォーマットの中でよく使われているBase64であれば聞いたことがある方も多いと思います。
Base64とはバイナリデータを文字列で表す為に使われるエンコーディングで、6ビットずつ64種類ある文字や記号に割り当ててエンコーディングするというものです。
Base58は言わばBase64の改良版で、以下のようなメリットがあります。
- 0（ゼロ）やO（オー）やI（アイ）やｌ（エル）などフォントによってはまったく区別できない紛らわしい文字を外したので、エンコード結果の文字列の判別がし易い
- +（プラス）など記号を使っていないので、エンコード結果の文字列をダブルクリックで一発で選択できて便利。
- 同じく記号を使わないことにより、エンコード結果の文字列が各種アプリで変に改行されたりしない。結果文字列をアカウント名として使用しやすい等のメリットもある
Base64はエンコーディング結果の文字列を人間が扱ったりしないので、別に見た目がどうなろうとダブルクリックで選択できなかろうと大した問題ではなかったのですが、Base58は人間に扱われることを踏まえて、上記のようなメリットを持つべくデザインされたということだと思います。
では実装していきたいと思います。ここでは以下のページを参考にしました。
Base58Check encoding – Bitcoin Wiki
Bitcoinで使われる技術要素 – Qiita
以下は、与えられたバイト列をBase58でエンコーディングした文字列にして返してくれる関数です。
public static string GetBase58EncodedString(byte[] byteArray)
{
var result = new StringBuilder();
string base58String = "123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz";
uint countOfZero = 0;
for (int i = 0; i < byteArray.Length; i++)
{
if (byteArray[i] == 0)
countOfZero++;
else
break;
}
var bl = new List<byte>(byteArray);
bl.Reverse();
var x = new BigInteger(bl.ToArray());
while (x > 0)
{
var r = (int)(x % 58);
x = x / 58;
result.Append(base58String[r]);
}
for (int i = 0; i < countOfZero; i++)
result.Append("1");
return new string(result.ToString().Reverse().ToArray());
}
特別な解説の必要はないと思いますが、与えられたバイト列をBigIntegerに変換して、それを58で割りながら余りの数をインデックスにしてどんどん対象の文字列から文字を拾ってくる感じです。また、与えられたバイト列の先頭に0x00があった場合は、その数に合わせて1を結果に追加しています。
Base58Check
ビットコインでは正確に言うとBase58Checkが使われているのですが、これはBase58と違うエンコーディング形式ということではなく、上で求めたチェックサムを公開鍵のハッシュ（バージョンバイト付き）と一緒にBase58エンコーディングをして、そこに誤り検知の機能を持たせることをもってしてそう呼んでいるようです。
この誤り検知につきましては、また別の記事ででも解説できたらと思いますが、基本的にはビットコインアドレスを手で入力したときに、打ち間違って違う送付先にビットコインを送ってしまうなどの事故を防ぐためのものです。
ビットコインアドレスを求める
いよいよ長かったこの記事にもついにこの瞬間がやってきました。ビットコインアドレスとなる文字列を、Base58エンコーディングによって求めます。
上述の通りチェックサムをくっつけてからBase58エンコーディングを行います。具体的に言うと、以下の25バイトのバイト列をBase58エンコーディングすることになります。
[21バイト 公開鍵のハッシュ（バージョンバイト付き）][4バイト チェックサム]
ではコードで求めてみましょう。
var base58Target = new byte[25];
Array.Copy(pubKeyHashWithVersion, 0, base58Target, 0, 21);
Array.Copy(checkSum, 0, base58Target, 21, 4);
string bitcoinAddress = Helper.GetBase58EncodedString(base58Target);
Console.WriteLine(bitcoinAddress);
以下、出力結果です。
1EohnzQdSSSsarBSncpHnfWxCzqSVZ3uPj
ついにビットコインアドレスが求められました！
これは正真正銘のビットコインアドレスであり、当然ビットコインを送付することも可能です。もちろん冒頭で書いた通り秘密鍵がばれてしまっているので、ここに送ったコインは簡単に盗まれてしまいますが、実験的に現在の価格で500円くらいのビットコインを送付してみました。
blockchain.infoでこのアドレスに関するトランザクションなどの情報を見ることが出来ます。
まとめ
秘密鍵からはじまり、公開鍵、公開鍵のハッシュのハッシュの作成、そして最後にビットコインアドレスを作るまでの過程を通してその裏にある技術的な知識を学びました。
今度続編を書く機会があれば、ではこのビットコインアドレスに送ったビットコインは、どうしてそのアドレスの持ち主（正確に言うと秘密鍵の持ち主）にだけ所有権があると保証されるのか、その部分について書きたいと思います。
あんまり記事が長くなり過ぎるのも嫌だったのと、まだ自分が勉強中のこともあってかなり色々な事を端折っています。もし「この部分が分かりづらい」などのご意見がありましたら、コメント欄ででもお知らせ下さい。
コード
using System;
using System.Collections;
using System.Collections.Generic;
using System.Linq;
using System.Numerics;
using System.Security.Cryptography;
using System.Text;
namespace MakeBitcoinAddress
{
class ECPoint
{
public BigInteger x = 0;
public BigInteger y = 0;
}
static class Helper
{
public static BigInteger Mod(BigInteger value, BigInteger modulus)
{
var result = BigInteger.ModPow(value, 1, modulus);
return (result < 0) ? result + modulus : result;
}
public static BigInteger ModInverse(BigInteger value, BigInteger modulus)
{
if (value < 0)
{
value = Helper.Mod(value, modulus) + modulus;
}
BigInteger x = 0, y = 1, gcd = modulus;
BigInteger px = 1, py = 0, pgcd = value;
BigInteger temp = 0;
while (gcd > 0)
{
BigInteger quotient = pgcd / gcd;
temp = x;
x = px - quotient * temp;
px = temp;
temp = y;
y = py - quotient * temp;
py = temp;
temp = gcd;
gcd = pgcd - quotient * temp;
pgcd = temp;
}
return px;
}
public static string GetBinaryString(byte[] byteArray)
{
string result = string.Empty;
for (int i = 0; i < byteArray.Length; i++)
{
byte b = byteArray[i];
if ((b == 0) && (i == byteArray.Length - 1))
{
break;
}
string binaryString = Convert.ToString(b, 2);
if (i < byteArray.Length - 1)
{
while (binaryString.Length < 8)
{
binaryString = "0" + binaryString;
}
}
result = binaryString + result;
}
return result;
}
public static string ByteArrayToString(byte[] ba)
{
StringBuilder hex = new StringBuilder(ba.Length * 2);
foreach (var b in ba)
{
hex.AppendFormat("{0:X2}", b);
}
return hex.ToString();
}
public static string GetBase58EncodedString(byte[] byteArray)
{
var result = new StringBuilder();
string base58String = "123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz";
uint countOfZero = 0;
for (int i = 0; i < byteArray.Length; i++)
{
if (byteArray[i] == 0)
countOfZero++;
else
break;
}
var bl = new List<byte>(byteArray);
bl.Reverse();
var x = new BigInteger(bl.ToArray());
while (x > 0)
{
var r = (int)(x % 58);
x = x / 58;
result.Append(base58String[r]);
}
for (int i = 0; i < countOfZero; i++)
result.Append("1");
return new string(result.ToString().Reverse().ToArray());
}
}
class Program
{
static BigInteger ModP = BigInteger.Parse("115792089237316195423570985008687907853269984665640564039457584007908834671663");
static ECPoint G = new ECPoint()
{
x = BigInteger.Parse("55066263022277343669578718895168534326250603453777594175500187360389116729240"),
y = BigInteger.Parse("32670510020758816978083085130507043184471273380659243275938904335757337482424")
};
static ECPoint ECAdd(ECPoint p, ECPoint q)
{
ECPoint result = new ECPoint();
BigInteger lambda = (q.y - p.y) * Helper.ModInverse((q.x - p.x), ModP);
result.x = BigInteger.Pow(lambda, 2) - p.x - q.x;
result.x = Helper.Mod(result.x, ModP);
result.y = lambda * (p.x - result.x) - p.y;
result.y = Helper.Mod(result.y, ModP);
return result;
}
static ECPoint ECDouble(ECPoint p)
{
ECPoint result = new ECPoint();
BigInteger lambda = (3 * BigInteger.Pow(p.x, 2)) * Helper.ModInverse((2 * p.y), ModP);
result.x = BigInteger.Pow(lambda, 2) - (2 * p.x);
result.x = Helper.Mod(result.x, ModP);
result.y = lambda * (p.x - result.x) - p.y;
result.y = Helper.Mod(result.y, ModP);
return result;
}
static ECPoint ECScalar(ECPoint p, BigInteger scalar)
{
ECPoint result = new ECPoint() { x = p.x, y = p.y };
string s = Helper.GetBinaryString(scalar.ToByteArray());
foreach(var c in s.Substring(1))
{
result = ECDouble(result);
if (c.Equals('1'))
{
result = ECAdd(result, p);
}
}
return result;
}
static bool IsOnSecp256k1(ECPoint p)
{
var answer = Helper.Mod((BigInteger.Pow(p.y, 2) - BigInteger.Pow(p.x, 3) - 7), ModP);
return (answer == 0);
}
static void Main(string[] args)
{
BigInteger k = 2017101920171019;
var publicKey = ECScalar(G, k);
byte[] inputBytes = new byte[65];
Array.Copy(new byte[1] { 0x04 }, 0, inputBytes, 0, 1);
byte[] x = publicKey.x.ToByteArray();
Array.Reverse(x);
byte[] y = publicKey.y.ToByteArray();
Array.Reverse(y);
Array.Copy(x, 0, inputBytes, 1, 32);
Array.Copy(y, 0, inputBytes, 33, 32);
SHA256 sha256 = new SHA256CryptoServiceProvider();
RIPEMD160Managed ripemd160 = new RIPEMD160Managed();
var publicKeyHash = ripemd160.ComputeHash(sha256.ComputeHash(inputBytes));
var pubKeyHashWithVersion = new byte[21];
Array.Copy(new byte[1] { 0x00 }, 0, pubKeyHashWithVersion, 0, 1);
Array.Copy(publicKeyHash, 0, pubKeyHashWithVersion, 1, 20);
var checkSum = sha256.ComputeHash(sha256.ComputeHash(pubKeyHashWithVersion)).Take(4).ToArray();
var base58Target = new byte[25];
Array.Copy(pubKeyHashWithVersion, 0, base58Target, 0, 21);
Array.Copy(checkSum, 0, base58Target, 21, 4);
string bitcoinAddress = Helper.GetBase58EncodedString(base58Target);
Console.WriteLine(bitcoinAddress);
}
}
}
参照
ビットコインのトランザクションについて
楕円暗号曲線や楕円曲線DSAについて
ビットコインの仕様について
